Everything in this blog post will be about those uniquely fascinating numbers known as prime numbers. I will be explaining how to build something known as the Sieve of Eratosthenes, which I will explain in detail later. The sieve will be able to spit out all the prime numbers between 2 and an arbitrarily large number of the user’s choosing. And speaking of prime numbers, I would like to briefly introduce them now because I do not want to gloss over anything from the beginning, this way the logic will make sense for when we actually begin building.
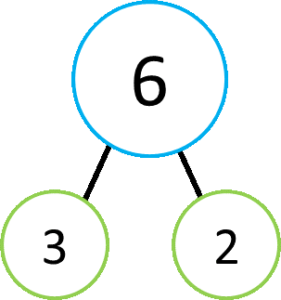
Prime numbers are numbers that are only evenly divisible by 1 and themselves. Or, as Wikipedia has it: “is a natural number greater than 1 that has no positive divisors other than 1 and itself.” Every other number is considered a composite because they are composed of prime numbers. Take the example of the number six. Six is not prime since it can be divided into evenly by both 2 and 3. Here is an example of a factor tree for the number 6, you can see it is broken down into its prime factors. (This can be read as 2 x 3 gets you to six).
Another example using the number 542:
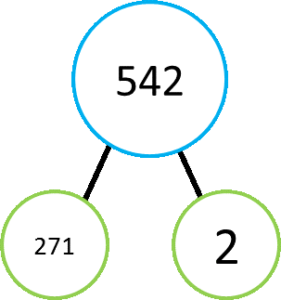
In this case, the composite number 542 can be broken down into its prime factors of 2 and 271 (271 is a prime number and therefore cannot be factored into smaller numbers). 2 x 271 = 542. Every composite number will have prime factors and that should make some sort of intuitive sense because if a number is not prime it is divisible by other numbers and therefore it can be written as a factor of other numbers. This can continue until the factors themselves are not divisible by smaller numbers and of course we call those primes. Perhaps it is easier to think about starting at the bottom, imagine taking a small prime number and multiplying that number by any other number of your choice, the result of that multiplication will be a composite number and one of its prime factors will be the prime that you had chosen. Take for example 7 x 3, the result is 21 and the prime factors of 21 are indeed 7 and 3. But what about 7 x 4, this results in 28 which can be factored down to 7 x 2 x 2. How about a random, large number as an example. 431 is a prime number so lets multiply that by a 2, then a 4 then a 6.
431 x 2 x 4 x 6 = 20,688
And what are the prime factors for 20,688?

As you can see there are a lot of 2’s and a 3 but also the original 431 is a prime factor as well, this must be by definition because we built a composite using 431 and therefore, as we deconstruct the composite number the prime we used must come out wholly intact. Think of primes as the smallest, indivisible pieces used to construct composite numbers. For that very reason, every single natural number can be factored down to its prime factors, run a few examples yourself if you like but every single natural number in existence can be expressed as the multiplication of primes unless of course the natural number in question is itself prime. Primes are the bricks used to build all the numbers you see around you. I feel that this is important to note because later on I will be using some shortcuts and they won’t make sense unless you have an understanding of primes and how they relate to composite numbers.
One more final point before we actually dive in and open up a spreadsheet: there are an infinite number of prime numbers. I found this concept difficult to grasp for a few reasons but it is nonetheless true. Surely, a number of sufficient size would be divisible by a lower number at some point? A monster of a number with thousands, or even trillions, of digits would surely have to be so large, and the amount of numbers below it so plentiful, that something should be able to divide into it evenly? But the answer is no, there are an infinite number of primes and the proof is actually quite simple to walk through. It is worth taking a moment to look at here.
Let’s make an assumption that there is a largest prime number and let’s call that number �. Now, take all the prime numbers up to and including � and multiply them all together. This will create some large composite number, let’s call this new number �. Now, � will be divisible by any one of the prime numbers we multiplied together to create it so it won’t be a prime number but what about the case for �+1? Because �+1 will not be evenly divisible by one of the primes multiplied together to create � (we saw to that by adding the 1) we can ask, is �+1 a prime number? Well, if there are no prime factors for �+1 then it would indeed have to be a prime number and also larger than �, which contradicts our assumption that � was the largest prime. If �+1 isn’t a prime number than it will certainly have prime factors but any prime factor would also be larger than � (remember, we already ruled out any primes up to and including P being able to divide evenly into �+1), also contradicting the assumption that there is a largest prime. So, either R + 1 prime and larger than the assumed largest prime, or it isn’t but it has a prime factor larger than the assumed largest prime. Both cases violate the assumption that there exists a “largest” prime number. There are, in fact, an infinite number of them. Try for yourself making the assumption that the largest prime is 23:
�=23
�=2∗3∗5∗7∗11∗13∗17∗19∗23=223092870
That number will be evenly divisible by any of those smaller primes we just multiplied together. Now add 1:
�+1=223092871
Is that number prime? No but the smallest prime factor, which you can find by using trial division, is 317. 317 is a prime number and larger than the assumed “largest prime” of 23. Had we used trial division and not found any number that could divide evenly into �+1, then of course the conclusion is reached that �+1 is itself a prime number. In either case we can always find a prime number larger than the assumed largest.
In an even simpler case, try this with 11.
�=11
�=2∗3∗5∗7∗11=2310
Again, 2310 will be divisible by any of those smaller primes, now add one:
�+1=2311
And you can test again but 2311 is actually a prime number. So we have seen two ways in which the largest prime assumption fails, and it will always fail.
Anyway, without further ado, lets talk about The Sieve of Eratosthenes.
Eratosthenes was a mathematician who lived in ancient Greece and is proof that people have been interested in prime numbers for millennia. He was born in 276 BCE and is possibly most famous for being the first to calculate the circumference of the Earth. In addition to that remarkable feat, he also invented geography and a very simple algorithm to suss out prime numbers up to an arbitrary limit, it is this algorithm that we will be using in Excel today. It is simple in its elegance, instead of testing to see whether each number is prime by dividing by all the numbers below it and looking for a divisor that doesn’t leave a remainder, this takes the opposite approach. It starts with the first prime number, 2, and lists all the multiples of 2 and marks them as composite. Then it looks at the next number and if it is a multiple of 2 (or any lower prime) it skips that number and moves on. If the next number hasn’t been marked as a multiple of anything below it then the algorithm knows it must be prime and will calculate all the multiples of that number. Once it gets up to the desired end point, there should be some gaps in the number sequence and these will all be prime since they have not been marked as multiples of anything.
The desired end point we will call �, � being any number you like. � can be so incredibly massive and yet this method will still find all the prime numbers below it in theory. In practice, computers have limitations and we are going to be building this in Excel which can handle quite large amounts of data, but nothing like what can be done utilizing many computers with massive processing capabilities. For instance, the current (as of this writing [January 2018]) largest known prime number is 2^{7}^{7}^, ^2^3^2^, ^9^1^7 – 1 and you can read more about it here. That number has a total of 23,249,425 digits, Obviously, this is far, far too big for Excel to handle. None the less, we can build a really cool working sieve and still learn a lot in the process even if we aren’t breaking any records.
Here is how the sieve will work in Excel, first it places a number, always starting with 2, which is prime. Then it will calculate all the multiples of 2 up to �, the desired number we asked the program to run up to. After placing all the multiples of 2 (4,6,8,10…) it will move on to the next number. However, there is no next number yet because 3 has not been calculated, it is not a multiple of 2. The computer will acknowledge this and say that 2+1 is an empty cell and therefore that number must be prime because it is not a multiple of a number below it. It will generate the 3 and begin calculating all the multiples of 3, placing them in their appropriate cells as it goes, all the way up to �. Next it will check 3+1 which already exists as 4 is a multiple of 2, the program determines that 4 is not a prime number and therefore does not need to calculate all the multiples of 4. Next is 4+1 which is again and empty cell, this must be prime and 5 is in fact a prime number. The program inserts all multiples of 5 (5,10,15,20…) up to �. It is very simple, elegant, and easy to comprehend.
There is an additional short cut we can take here, after finding a new prime we can actually square it and begin listing the multiples from there. We can get away with this because the multiples of the prime between itself and its square will already have been marked as composite. Once we find 7, for instance, we can square it and go right to 49, then 56, 63, etc. You will notice that 7 x 2 (14) is already in the list of numbers because we already calculated 2 x 7. And of course there is no need to recalculate 7 x 3 because we already placed the multiples of 3 including 3 x 7 which is why 21 is already listed as composite as well. How about 7 x 4 for 28? We didn’t actually calculate all the multiples of 4 because it isn’t prime but we did calculate all the multiples of the prime factors of 4, which is simply 2 x 2. So 2 x 2 x 7 = 4 x 7 = 28. This will work for all the multiples between the new prime and its square as you can see when the program begins plugging in the numbers. So we don’t need to do 7 x 6 for 42 because the prime factors of 6 are 2 and 3 and those multiples have been calculated and placed into the grid. 2 x 3 x 7 = 6 x 7 = 42. This will save a lot of time because now we no longer have to calculate the multiples of all primes below �, we just need to find the multiples of all primes below �. For example: � is 100. The program will run until number is greater than 100 which is 10. There is no need to calculate 112 because that is 121 which is larger than we need. You will notice that once it hits 10 and stops there will still be a lot of holes in the number grid but we can say with certainty that the holes are there because they are not a multiple of any lower number and therefore they are all primes, all the program has to do now to finish is fill in the holes and mark them as prime.
This is what it will look like when it is finished and functional:
There are quite a few variables this time around so I’ll just paste them in now and go over them one by one:
Dim prime As Double
Dim prime2 As Double
Dim startx As Double
Dim starty As Double
Dim toplim As Double
Dim r2 As Double
Dim rcol As Integer
Dim gcol As Integer
Dim bcol As Integer
The first thing you might notice is the variable type, that’s not something I have talked about before and it is worth mentioning. Because the numbers involved here will get very large we have to make sure we allocate enough space for them. The variable type Integer only accepts integers up to 32,777 and we will fly past that limitation pretty quickly. For instance, there are over 78,498 primes between 2 and 1,000,000 and if we store them in a column we will breach that limit with our row variable. The type Double allows integers and numbers with decimals all the way up to around 1.7+E308. They will take up more memory and therefore make things a bit slower but that shouldn’t be too much of a concern right now.
Prime is what I will use to hold any number that is determined to be prime. Prime2 will be that same prime number squared. startx and starty will be the row and column position variables used when the system finds a new prime and needs to know where to go next. toplim is the user-entered upper limit that they want to know the primes below of. If they want a list of all primes numbers below 10,000 then they enter 10,000 and toplim will take on that value. r2 is the row index for where excel will store the list of generated primes. Finally, rcol, gcol, and bcol are color variables for r, g, b values and they will each be between 0 and 255 so they need only be Integer type.
Tthe next subroutines will generate a list of numbers from left to right and top to bottom, 10 numbers wide. 1 to 10 in row one from cells (1,1) to (1,10). 11 to 20 in row 2 from cells (2,1) to (2,10); 21 to 30 in row 3, etc. It will change the cell color so that all multiples of a certain prime will have the same color and it will color the prime numbers in red text. Finally, it will create a list of the discovered primes in column 13.
The first sub routine will request the upper limit from the user before setting up the main loop. The loop will canvas the number grid area, moving from left to right and top to bottom and in sequentially ascending order. Any empty spaces will be determined prime and filled in before calling a sub routine to handle the multiples of the new prime, any spaces already containing numbers will be determined not prime and skipped over. It will do this until it reaches the square root of the toplim variable then it will call the final sub routine, named fill, which will quickly race over the entirety of the number grid, plugging in any remaining holes and adding them to the list of primes in column 13.
This subroutine has some variables specific to only itself: r, c, and numbs. If you haven’t already guessed, r is for row and c is for column, numbs takes on a number value which is determined by r and c and will progress over the numbers until it reaches the square of toplim and the program breaks the loop. The following should look pretty straight forward but I’ll go over in detail anyway, the first thing that should jump out at you however is that c (for column) starts at 2 while r (for row) starts at a healthy 1. This is because the first prime number is 2 and 1 would make things very messy. If c started at 1, the program would determine cells(1,1) to be empty and place in the number 1 before proceeding to place all the multiples of 1, which is of course every number. So the sieve starts with 2 and the program begins by testing cells(1,2) for a value.
Sub start()
toplim = Application.InputBox(“Please enter the highest number”)
r = 1
r2 = 1
c = 2
prime = 1
numbs = 1
Do Until numbs > Sqr(toplim)
If Cells(r, c).Value = “” Then
prime = c + ((r – 1) * 10)
Cells(r, c).Value = prime
Cells(r, c).Font.ColorIndex = 3
Cells(r, c).Font.Bold = True
Cells(r2, 13).Value = prime
rcol = Int((255 – 0 + 1) * Rnd + 0)
gcol = Int((255 – 0 + 1) * Rnd + 0)
bcol = Int((255 – 0 + 1) * Rnd + 0)
Cells(r, c).Interior.color = RGB(rcol, gcol, bcol)
Cells(r2, 13).Interior.color = RGB(rcol, gcol, bcol)
r2 = r2 + 1
Call primer
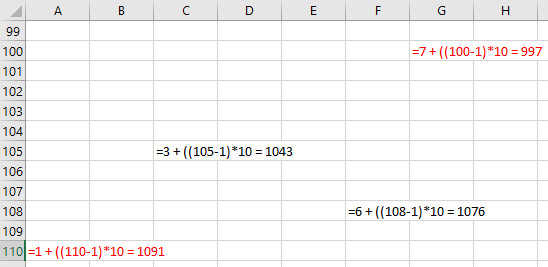
Now to unpack what is happening up there, the system looks for a value in cells(r,c) which is cells(1,2) to start. It will determine this to be empty, naturally. Now it knows it has found a prime number but it doesn’t know the number yet and needs a way to devise it and because the grid is simple and uniform it can tell what number goes where based on the cell address. That is what this line does: prime = c + ((r – 1) * 10). All it has to do is adjust the row down by 1 and then add the column value in order to extract the correct value that belongs in the position. So upon discovering cells(1,2) is empty: Prime = 2 + ((1-1)*10) which gives us the answer 2. Excellent, the first prime is 2. Another example, eventually the program stumbles across and empty cell where the prime number 23 should be. Prime = 3 + (3-1)*10) which gives the answer 23 (recall, the 1’s are in row 1, 10’s in row 2, 20’s in row 3, etc.) How about if the program finds an empty cell in row 109 and in column 1? Well, prime = 1 + ((110 – 1)*10 = 1091. And 1091 is prime, it calls the subroutine that handles the next procedures once again. Here is a screen shot showing how that math looks, primes are in red:
Else:
c = c + 1
If c > 10 Then
c = 1
r = r + 1
End If
End If
This will make sure that the program moves on to the next number sequentially. It does so by evaluating the cell directly to the right of the previous cell in the same row, if c were 2 then c will become 3. However, if c were 10 then the program will find itself on the extreme right-hand side of the number grid, instead of increasing c up to 11 it simply forces c back down to 1 but it increases the row value by 1. This ensures that it obeys the following pattern:
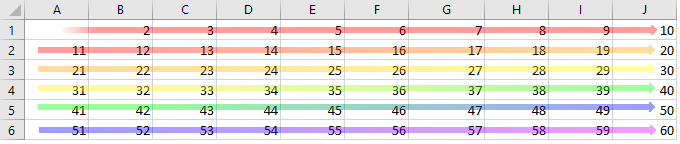
Again, make sure that numbs increases to the next value that has been evaluated and call the loop back. If numbs is greater than the root of toplim, the loop breaks and we can be satisfied that the program has calculated all the multiples required of it. After all of that there will only be one more routine to run and that is called fill, which fills in the remaining holes in the grid. Be sure to code those in at the end of the routine “start.”
numbs = c + ((r – 1) * 10)
Loop
Call fill
End Sub
“Fill” is the final step, lets first look at the other steps beginning with where the program goes after discovering, coloring, and placing a new prime.
The second routine, called primer, will take the newly discovered prime, square it, then place that number in the appropriate position in the number grid. This is where we will be using primep, startx, and starty; they will be giving us the x and y coordinates to place the squared prime known as prime2. First we shall calculate the row to place prime2 and the row value will be stored in startx. Since we are using rows of ten numbers all we really need to do is figure out how many 10’s are in prime2 then add 1 to that number which will get us startx. To do this, set primep equal to the integer of prime2 over 10. This gives us the number of 10’s in prime2: 49/10 = 4.9 and because we are taking the integer of the answer it will drop anything beyond the decimal (in actuality it rounds the number down to the nearest whole number), so primep will = 4 then we add 1 and get a startx of 5. And indeed, 49 belongs in the 5th row. In the case of the prime number 2, 22 is 4 and 4 / 10 is .4, taking that integer gives us a 0. Add 1 and we have determined that the number 4 belongs somewhere in row 1. 832? Well that equals 6889, take the integer of that divided by 10 and the answer is 688, add 1 and startx will take on the value of 689 and that is exactly the row the 832 belongs in. Now for the columns and starty: starty will simply be equal to the ones place value of prime2 because the number grid we are building is nice and simple, anything ending in a 6 should go in column 6, if it ends in 1 then it belongs in column 1 etc. So, as per the previous example, 6889 belongs in column 9. There are many, many ways to extract that value from a number but I chose this method: have prime2 subtract off a primep that has been multiplied by 10 and this will always give the value in the ones place. So, for example, 6889 – (689 * 10) = 9. 121 – (12*10) = 1 And of course this works for the smaller number as well. 4 – (0*10) just gives us 4 and a 4 undoubtedly belongs in column 4. Finally, before leaving the sub routine, make sure to color the cell and off we go, the prime has been squared and that number has been placed in its proper location, here is everything I just explained in the VBA code:
Sub primer()
prime2 = prime ^ 2
primep = Int(prime2 / 10)
startx = 1 + primep
starty = prime2 – (primep * 10)
Cells(startx, starty).Value = prime2
Cells(startx, starty).Interior.color = RGB(rcol, gcol, bcol)
Call composite
End Sub
Next there must be a sub routine to create all the multiples of the new prime number from its square up to �. I called this routine composite, lets take a look:
Sub composite()
num = prime + prime2
x = startx
y = starty
Do Until num > toplim
y = num Mod 10
x = Int(num / 10)
If num Mod 10 = 0 Then x = x – 1
If y = 0 Then y = 10
Cells(1 + x, y).Value = num
Cells(1 + x, y).Interior.color = RGB(rcol, gcol, bcol)
num = num + prime
Loop
End Sub
Seems simple enough, I shall break it down to explain exactly what is happening and why. The machine already has prime (which will be 2 or 7 or 23, etc.) and it also has prime2 (which is just prime squared) so the next multiple of prime that needs to be placed is prime2 + prime. For example, lets say the newly discovered prime was 7, the routine “primer” will square 7 and place 49 so the next multiple will be 49 + 7, or 56. After that all the program needs to do is keep adding prime to that number and I called that number “num” (num = prime2 + prime). Now, if prime is 11 then prime2 + prime will be 132 so num will be equal to 132 and after each loop all we need to do is make sure that prime is added to num. From 132 to 143, 154, 165… That is how the program knows the multiples but it still needs a way to figure out where they live. If the program can find the value of a number based on its cell address, so to can it determine the cell’s address based on the number, and it already has the number. Much like the previous function, this one will use the ones and tens places to figure out where to place it. First we will pluck out the value of the ones place in order to determine the column value called y. Simply divide num by 10 and take the remainder. This is what the Mod function achieves. X Mod Y gives the remainder of X / Y. So 49 Mod 10 would equal 9 (49 divided by 10 would leave a remainder of 9); 49 belongs in column 9. 33 / 10 gives a remainder of 3 so 33 belongs in column 3. Just like we have done earlier, the row value, x, is determined by the number of 10’s in num. Sticking with the previous examples, if num is 49 then int(49/10) = 4. Int(33/10) = 3 These numbers belong in rows 5 and 4 respectively and they will be adjusted up by 1 in the final calculation: Cells(1 + x, y).Value = num. There is just a slight adjustment that has to be made before finishing off this sub routine and it arises because anything multiple of 10 will alter the pattern we are building. Consider the number 40: 40 Mod 10 = 0 so Excel will try to place this number in column 0 which will crash the program. 40/10 = 4 so the program would also place this number in a row too high by 1. The simple solution here is to just tell Excel where we want 10’s to be placed, if y = 0 then we actually want y = 10 and if num Mod 10 = 0 then adjust x down by 1 as well. A very simple fix indeed and you can see that being done in the if statements in the above code. Once the correct cell address has been figured out have the program place the multiple and color in the cell before adding prime to num and looping again.
Sub fill()
r1 = 1
c1 = 2
Do Until c1 + ((r1 – 1) * 10) > toplim
If Cells(r1, c1).Value = “” Then
Cells(r1, c1).Value = c1 + ((r1 – 1) * 10)
Cells(r1, c1).Interior.ColorIndex = 5
Cells(r1, c1).Font.ColorIndex = 3
Cells(r1, c1).Font.Bold = True
Cells(r2, 13).Value = Cells(r1, c1).Value
r2 = r2 + 1
End If
c1 = c1 + 1
If c1 > 10 Then
c1 = 1
r1 = r1 + 1
End If
Loop
End Sub
Fill’s function is very similar to the macro “start”’s except all the multiples have been calculated so it will simply run over all the cells filling in the empty ones with the appropriate number and mark them as prime before adding them to the list in column 13. This one also loops until it reaches a number larger than toplimand it will also format the primes as “start” did (red and bold). The only real difference is that it won’t generate a new color for each prime because none of the multiples will need to be calculated, I chose to make all these filled in primes a uniform blue but you can use whatever color you fancy.
Finally, place a button on the sheet you would like the sieve to run on and set it to initiate the macro “start”
by right clicking on the button and clicking on “assign macro.” After clicking the button, enter your desired � and a beautiful mosaic of colors and number should begin to materialize on the sheet. Following the colors down the grid, some pretty obvious patterns should emerge. Like the multiples of…
2:
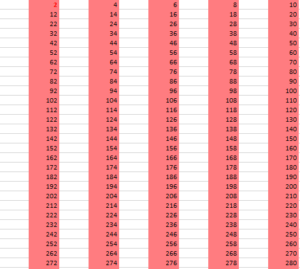
3:
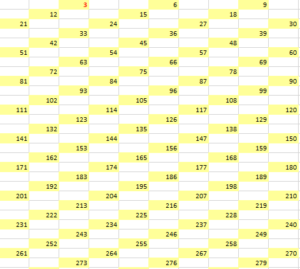
7:

23:

83:

But scrolling down through the primes, no obvious pattern emerges.
The distribution of the primes among the natural numbers has fascinated mathematicians for centuries and there are some methods that explain the distribution approximately but if you can see a pattern and explain this distribution exactly…
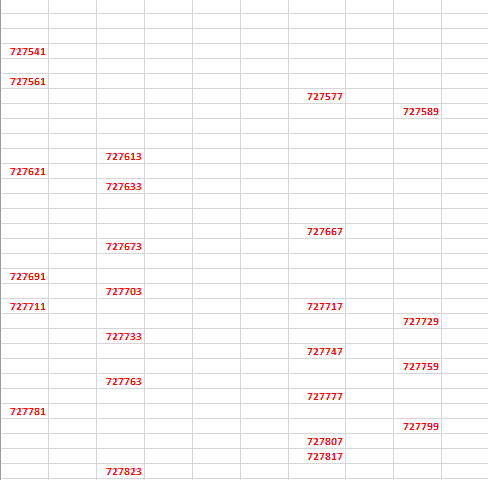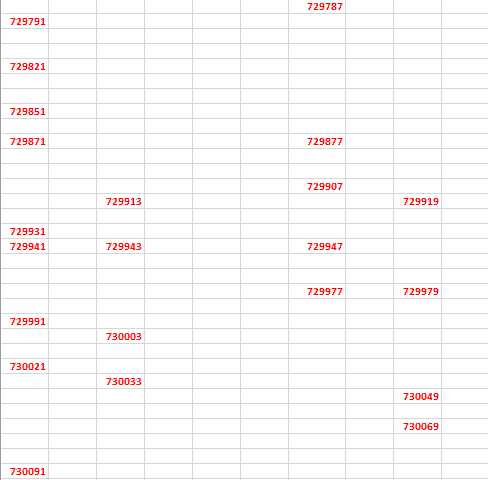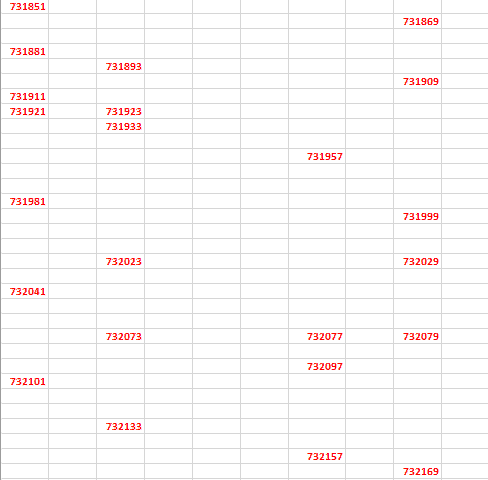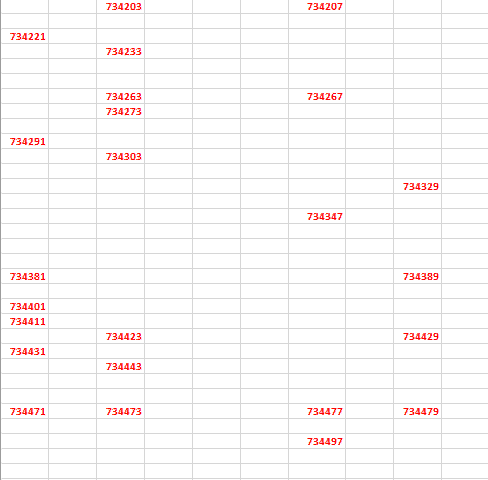
…you might be able to solve one of the most classical problems in mathematics.
Download sheet: