The logic problem goes as follows:
” There are one hundred prisoners, each numbered one through one hundred. In an adjacent room, there are 100 boxes, also numbered one through one hundred. Each box holds a slip of paper, also numbered one through one hundred however each slip of paper is randomly inserted into each box. For example, box five may hold paper number thirty-eight. Box number ninety-nine may hold paper forty, etc. Each prisoner will enter the room and look for their own number on a piece of paper. They may look in any box, but they may look in a maximum of fifty boxes. If they find their slip, they may exit the room, victorious. All boxes are closed at the end of each trial before the next prisoner enters. No prisoner may communicate with another once the trials have started. If all one hundred prisoners find the piece of paper with their own numbers on it, they all go free. If even one prisoner fails, they will all be executed. “

The most obvious, though ineffective, strategy is to simply choose fifty boxes at random and hope you find your ticket. Some will, some won’t. In fact, about half of the prisoners would be expected to find their own numbers this way. This, however, is not nearly enough to save all of them.
If the probability that an individual finds theirs is 1/2. The probability that everyone finds theirs is 1/2 * 1/2 *1/2….100 times. This results in a probability of…
![]()
Which is staggeringly low, though, not impossible.
Given sufficient trials, that strategy would work in one or some of them. Anything that isn’t forbidden is compulsory given sufficient time.
Let’s write down the code and run a few trials using the above method. But first, I need a shuffle macro to deal with managing some of the code, so I will show that first as it will be called often.

Here is the code, It will take the numbers 1 to 100 and place them in random order, never repeating any number, in column two on the main sheet. Column one is ordered from 1 to 100 representing each box. Column two holds the papers inside the box, these are randomized so that box 1 may hold number 77, box 34 might hold number 58, etc. To help with this, I am using a data structure called a collection, which is similar to an array but also has some nice properties that are useful here. For example: they can have elements removed and will resize automatically. I will create a collection of numbers 1 to 100, then, in row one, I will have it choose a random number from the collection and insert it into row one. That number will then be removed from the collection. Next, I will have it enter a new random number in row 2, also then removing that number from the collection. By the end, the collection will have been reduced to nothing, and all the numbers will have been placed in a random order on the Excel sheet in rows 1 through 100. Comments to explain what each line does:
Sub shuffle()
'Call the randomize function.
Randomize
'Define a variable to hold the numbers up to 100.
Dim x As Long
'Define a new collection.
Dim numbers As New Collection
'A simple for loop. The .Add function adds the new element, number x, to the 'bottom of the collection.
For x = 1 To 100
numbers.Add x
Next x
'Loop for all 100 numbers to rearrange them all.
For y = 1 To 100
'Get a random number between 1 and the size of the collection. The collection 'will shrink as the loop runs, so after 40 iterations, the collection will only 'hold 60 numbers, etc.
rando = WorksheetFunction.RandBetween(1, numbers.Count)
'Set row number y equal to the random number from the collection.
Sheets("Main").Cells(y, 2).Value = numbers(rando)
'Delete that number from the collection so that it can't be used again.
numbers.Remove (rando)
'Increase y so that the next random number goes in the next row.
Next y
End SubThat code block shuffles the numbers held in each box. There is another shuffle function that is nearly identical, except that one simply makes a list of random numbers from 1 to 100 on another sheet. Since the prisoners may want to search the boxes at random, they should have a random list of numbers to follow that also ensures they won’t repeat the same search. You will see that in the macros should you download the sheet (at the bottom of this post).
Sub prisoners_random_trial()
'a number is needed for each prisoner, from 1 to 100, starting at 1
Dim prisoner As Long
'a number is needed for each box, from 1 to 100
Dim boxnum As Long
'a number is needed to keep track of how many tries, or simulations, there have 'been, starting at 1
Dim try As Long
'another number is needed to keep track of the row values
Dim x As Long
'success will increase each time a prisoner is successful in finding their 'number
Dim success As Long
success = 0
try = 1
'insert however many simulations you'd like to run
Do Until try > 10
prisoner = 1
'each prisoner gets a try and there are 100 of them
Do Until prisoner > 100
'x starts at row 1 in the sheet "RandomListForPrisoners" which holds vector of 'random numbers from 1 to 100
'this is how we can simulate the prisoner selecting a random box whithout ever 'selecting the same one twice,
'this will be the box that they look in.
x = 1
boxnum = Sheets("RandomListForPrisoners").Cells(x, 1).Value
'each prisoner gets 50 tries, loop until 50 or until they succeed
Do Until x > 50
'if they find their own number, break the loop by setting x higher than 50, 'increase "success" by 1
If Cells(boxnum, 2).Value = prisoner Then
x = 100
success = success + 1
Else
'if that box didn't hold their number, increase x by one, which means getting a 'new box value from the other sheet
'then loop again to see if the new box holds thier number.
x = x + 1
boxnum = Sheets("RandomListForPrisoners").Cells(x, 1).Value
End If
Loop
'after the prisoner has tried, whether successful or not, shuffle the list of 'numbers on sheet "RandomListForPrisoners"
'so that the next prisoner will look in a different, random order of boxes and 'increase the prisoner number by 1
'loop until all 100 prisoners have had a try.
Call shuffleBoxes
prisoner = prisoner + 1
Loop
'After all the prisoners have tried, check the value of success, if it is 100 'that means that all prisoners have been successful.
If success = 100 Then
Cells(try, 5).Value = "Complete"
Else
'if it was an overall failure, mark it as such and list the number of prisoners 'who did find their
'own number, the value stored in "success"
Cells(try, 5).Value = "Fail"
Cells(try, 6).Value = success
End If
'reset the success variabel, shuffle the box numbers that the prisoners will 'check in preparation of the next simulation,
'shuffle the papers in the boxes, and increase "try" by one as the next 'simulation is about to begin
success = 0
Call shuffleBoxes
Call shuffle
try = try + 1
Loop
End SubI ran the above simulation 1,000 times. As expected, none of the trials were successful, and half of the prisoners found their own number. Are they always destined to lose so catastrophically? Not quite! Let’s look at a method that can increase the odds of success dramatically.
Every prisoner should immediately check the box with their number in it. In the unlikely event that the box does indeed hold their number, they are finished. In the more likely event that it does not, they should then proceed to the box listed in the paper. For example: the prisoner is number 5 so they go to box 5. Box 5 holds paper number 11, so they proceed to box number 11. Box 11 holds paper number 9 so they go to box number 9. And so on, proceeding in this fashion until they have either found their own number, or exhausted all 50 tries.

This method will increase the rate of success from the pitifully small number earlier up to….

About 31%.
Though small, that is nearly a third, and worth trying if the alternative is certain death. Buy, why does it work? And will the simulation we build achieve the same result?
Within the room, there will be boxes linked by “loops” which can be smaller or larger. The loop in the image above is length 4, but you can easily imagine loops being length 5, 12, 47, 68, etc. But each loop will eventually lead back to first box opened.
This is why the prisoner must choose the box with their number on it initially as it guarantees that they will join a loop which contains their number. Some box must point back to the initial one they opened, or they would continue indefinitely. As there are a finite amount of boxes, that is impossible. So even if it is the 100th box that holds the prisoner’s number, and therefore the number of the box the prisoner started with, it is guaranteed to be found. Therefore, each prisoner is guaranteed to be on the correct loop for success and will be guaranteed to find their own number given sufficient tries. The limiting agent in this set is simply the allowed number of tries: 50.
The rest is up to random chance. If all the loops require 50 steps or less to complete, then the prisoners will be saved. If even one loop is 51 steps or greater, they will all fail. The only thing remaining to calculate is the probability that one chain is greater than 50 parts.
This requires combinations and probability, which shouldn’t be too difficult to figure out. But, first things first, we are talking about different ways of combining things. This suggests that we will be using factorials, I haven’t taken a tangent yet and this seems as good a place as any.
Factorials. X! As your comedic professor would point it, it means you yell the number really loud. Most of us know how to use them, you multiply each integer by the preceding integer on and again until reaching one.
But, did you know that behind these seemingly innocuous operators lies a more sinister beast, like a cobra, hiding beneath a boulder, waiting to strike…
![]()
The above is called the gamma function and is the generalized formula for factorials. I need to show that to talk about a property of them which, I think, is pretty cool. But first, it should also be noted that the above allows us to find values of the gamma function for rationals, all real numbers actually. So, when someone asks how you can possibly find the factorial or 1/2 or other fractions, you can point out that it is actually possible, indeed, the typical way most of us calculate factorials is actually just because they usually are of a very specific type: factorials of integers.
Another way to explain what a factorial measures, and why are often only used with integers for probability problems, is that the factorial is a measure of how many different ways a number of items can be arranges. For example: items A and B can be arranged in two ways:
While three items, can be arranged in six different ways:
While one item can only be arranged one way:

OK, so about that cool property: the factorial of zero is actually equal to one.
![]()
Which seems a little odd, because we used to calculate factorials like this:
3! = 3*(3-1)*(3-2) = 6.
2! = 2*(2-1) = 2.
1! = 1
So what happens at 0? It is possible to calculate it using the more general definition from earlier.
So, back to that integral definition and how we can use it to calculate the factorial of zero. First, we must prove a couple of things. If we can calculate the Gamma of 1, then prove that ![]() which would then prove that
which would then prove that ![]() . So lets try!
. So lets try!
Calculate the Gamma of 1:
![]()
![]()
Anything to the 0th power is equal to 1. So ![]() becomes 1
becomes 1
![]()
And that is an easy solve. Let ![]()
![]()
![]()
![]()
![]()
Ok, ok, we should probably use the more formal notation:
![]()
And the function ![]() is it’s own derivative, and therefore it’s own antiderivative, so that’s an easy solve:
is it’s own derivative, and therefore it’s own antiderivative, so that’s an easy solve:
![Rendered by QuickLaTeX.com \[=\lim_{b\to\infty} -\int_0^{b}e^{u} du = \lim_{b\to\infty} -e^{u}\Biggr|_{0}^{b}\]](https://lejavbasolutions.com/wp-content/ql-cache/quicklatex.com-675c5f521693edb89171b102f94cf9fb_l3.png)
Plug ![]() back into
back into ![]()
![Rendered by QuickLaTeX.com \[= \lim_{b\to\infty} -e^{-t}\Biggr|_{0}^{b}\]](https://lejavbasolutions.com/wp-content/ql-cache/quicklatex.com-71c5bccaae1c6eafd0893b12413dcb10_l3.png)
![]()
Evaluating that limit yields a 0 ( a 1 divided by a very, very large number equals a very small number. A 1 over infinity evaluates to 0).
![]()
And ![]() , like anything raised to the 0 power, is equal to 1. Then we would have 0 minus a negative 1, which is, of course, a positive 1.
, like anything raised to the 0 power, is equal to 1. Then we would have 0 minus a negative 1, which is, of course, a positive 1.
![]()
![]()
Ok, next step, proving that the Gamma function acts as the factorial. To do so, first consider the function ![]()
![]()
![]()
Let’s solve using IBP (integration by parts) and I will select ![]() to be my
to be my ![]() , therefore, to calculate the derivative of
, therefore, to calculate the derivative of ![]() you multiply by the exponent
you multiply by the exponent ![]() and then decrease the exponent by 1. For the
and then decrease the exponent by 1. For the ![]() function,
function, ![]() is set equal to
is set equal to ![]() which means that, after integrating,
which means that, after integrating, ![]() (you can do that one fairly easily using u-substitution with
(you can do that one fairly easily using u-substitution with ![]() . So:
. So:
![]()
![]()
![]()
![]()
![]()
Notice how the inegral is now the original gamma function? So, this can be rewritten:
![]()
The first term ![]() will be 0 at infinity, so that whole thing just disappears. Leaving just this final expression:
will be 0 at infinity, so that whole thing just disappears. Leaving just this final expression:
![]()
If ![]() then
then ![]() then we can daisy chain them all until getting back to the more commonly known definition of the factorial.
then we can daisy chain them all until getting back to the more commonly known definition of the factorial.
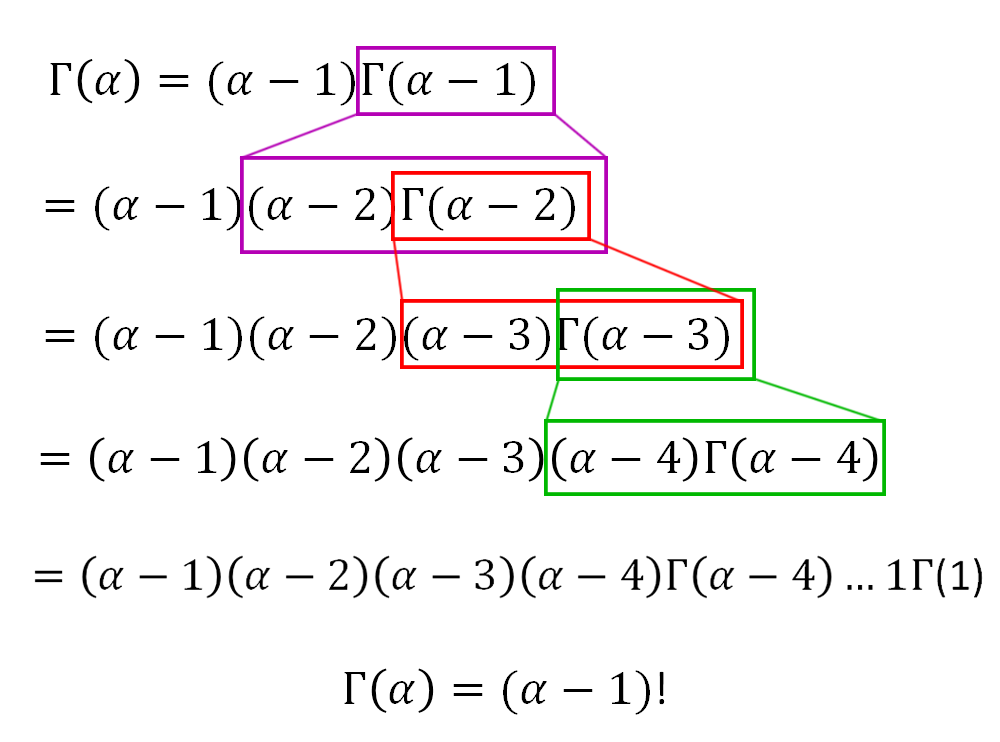
So it is pretty clear that:
![]()
Finally proving that:
![]()
And going back to the idea that a factorial is the number of ways items can be arranged, well, how many different ways can you arrange nothing? Only one way:

Thus ends the extended but fun tangent into factorials. We will see them pop up again in a moment when figuring out exactly why the odds increase for the 100 prisoners.
Better method:
Here is a brief overview of why the magic number is about 31%. As each prisoner has started with a box with their number on it, they will automatically be in the loop that, at some point, points back to their box. They will be successful so long as that loop is not greater than 50 boxes in length. So, given 100 boxes, what is the probability that out of all the loops, none of them are greater than 50?
Considering that there are 1 to 100 numbers, there can only be one loop larger than 50, in fact, for any number of these problem types, there can only ever be one loop greater than ![]() . Out of 100 boxes, there can be a loop of any size from 1 to 100. The number of ways to select a loop of any given size is given by the binomial coefficient:
. Out of 100 boxes, there can be a loop of any size from 1 to 100. The number of ways to select a loop of any given size is given by the binomial coefficient: ![]() which can be written using factorials like so
which can be written using factorials like so ![]() . Now we are seeing factorials in action, and this also explains why I went a bit mad exploring factorials above (does it though?). The binomial coefficient is the number of ways to select a combination of things from a larger set of things.
. Now we are seeing factorials in action, and this also explains why I went a bit mad exploring factorials above (does it though?). The binomial coefficient is the number of ways to select a combination of things from a larger set of things.
The probability of getting any one specific loop is, naturally, ![]() . The probability that the loop is 51in length is
. The probability that the loop is 51in length is ![]() . The probability that the loop random loop is not 51 boxes in length is
. The probability that the loop random loop is not 51 boxes in length is ![]() . Those 100 factorials will cancel leaving just
. Those 100 factorials will cancel leaving just ![]() or just over .98, meaning that is a roughly 98% chance of success so long as there isn’t a loop of exactly 51. Of course, the actual problem wants us to calculate the success rate if the loop is 51 or greater, to do so, simply add in those individual probabilities as well.
or just over .98, meaning that is a roughly 98% chance of success so long as there isn’t a loop of exactly 51. Of course, the actual problem wants us to calculate the success rate if the loop is 51 or greater, to do so, simply add in those individual probabilities as well.
![]()
If you factor the ![]() term into the parenthesis, all the
term into the parenthesis, all the ![]() terms will cancel leaving just:
terms will cancel leaving just:
![]()
And, as you might notice, the above is simply 1 minus a portion of the harmonic series! Specifically, the harmonic series between 51 and 100, or the harmonic number 100 minus the harmonic number 51: ![]() . You can do it by hand, or plug it into Excel, however you like but the results is:
. You can do it by hand, or plug it into Excel, however you like but the results is:
![]()
Meaning we are now predicting a success rate of about 31%. Time to test it!
The code will be nearly identical, the prisoners will just take a different tactic, so that is the only code that requires modification:
Do Until prisoner > 100
'This time, the first box selected will be the same number as the prisoner
boxnum = prisoner
x = 1
Do Until x > 50
'Check to see if the paper in the box is the same number as the prisoner.
'If they are equal, this prisoner is successful. Break the loop
'and increase success by one.
If Cells(boxnum, 2).Value = prisoner Then
x = 100
success = success + 1
Else
'If the numbers did not match, the next box to check should be the same number 'as that on the paper held by the box just opened. Get the value (held in the 'column just next to the box number, remember) and then use that as the next 'box number.
boxnum = Cells(boxnum, 2).Value
End If
'Increase x and try again if necessary.
x = x + 1
Loop
'increase the prisoner number by 1
'loop until all 100 prisoners have had a try.
prisoner = prisoner + 1
Loop
Note that because each prisoner doesn’t require a column of random numbers to decide which box to open next, that shuffle function never needs to be called. So this simulation will run much, much faster.
After running that simulation 1,000 times, the results are in:
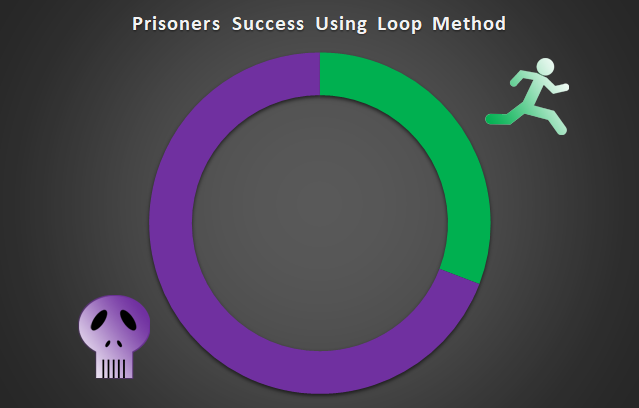
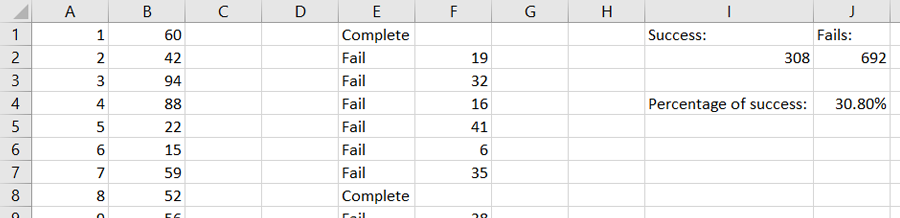
The final number I achieved is 0.308 or just over 30%, proving, once again, that statistics make accurate predictions. Should you ever find yourself in the predicament above, which hopefully never happens, you will know the best tactic to take.
It is extraordinarily unlikely to ever find yourself in such a situation, however, if you live long enough, and the universe manages to exist long enough, well, anything that isn’t forbidden is compulsory….
Full code, copy and paste into VBA module in your workbook.
Sub prisoners_smart_method()
‘Sub prisoners_random_trial()
‘a number is needed for each prisoner, from 1 to 100, starting at 1
Dim prisoner As Long
‘a number is needed for each box, from 1 to 100
Dim boxnum As Long
‘a number is needed to keep track of how many tries, or simulations, there have been, starting at 1
Dim try As Long
‘another number is needed to keep track of the row values
Dim x As Long
‘success will increase each time a prisoner is successful in finding their number
Dim success As Long
success = 0
try = 1
Do Until try > 10
prisoner = 1
Do Until prisoner > 100
boxnum = prisoner
x = 1
Do Until x > 50
If Cells(boxnum, 2).Value = prisoner Then
x = 100
success = success + 1
Else
boxnum = Cells(boxnum, 2).Value
End If
x = x + 1
Loop
prisoner = prisoner + 1
Loop
If success >= 100 Then
Cells(try, 5).Value = “Complete”
Else
Cells(try, 5).Value = “Fail”
Cells(try, 6).Value = success
End If
success = 0
Call shuffle
try = try + 1
Loop
End Sub
Sub prisoners_random_trial()
‘a number is needed for each prisoner, from 1 to 100, starting at 1
Dim prisoner As Long
‘a number is needed for each box, from 1 to 100
Dim boxnum As Long
‘a number is needed to keep track of how many tries, or simulations, there have been, starting at 1
Dim try As Long
‘another number is needed to keep track of the row values
Dim x As Long
‘success will increase each time a prisoner is successful in finding their number
Dim success As Long
success = 0
try = 1
‘insert however many simulations you’d like to run
Do Until try > 10
prisoner = 1
‘each prisoner gets a try and ther are 100 of them
Do Until prisoner > 100
‘x starts at row 1 in the sheet “RandomListForPrisoners” which holds vector of random numbers from 1 to 100
‘this is how we can simulate the prisoner selecting a random box whithout ever selecting the same one twice,
‘this will be the box that they look in.
x = 1
boxnum = Sheets(“RandomListForPrisoners”).Cells(x, 1).Value
‘each prisoner gets 50 tries, loop until 50 or until they succeed
Do Until x > 50
‘if they find their own number, break the loop by setting x higher than 50, increase “success” by 1
If Cells(boxnum, 2).Value = prisoner Then
x = 100
success = success + 1
Else
‘if that box didn’t hold their number, increase x by one, which means getting a new box value from the other sheet
‘then loop again to see if the new box holds thier number.
x = x + 1
boxnum = Sheets(“RandomListForPrisoners”).Cells(x, 1).Value
End If
Loop
‘after the prisoner has tried, wether successful or not, shuffle the list of numbers on sheet “RandomListForPrisoners”
‘so that the next prisoner will look in a different, random order of boxes and increase the prisoner number by 1
‘loop until all 100 prisoners have had a try.
Call shuffleBoxes
prisoner = prisoner + 1
Loop
‘After all the prisoners have tried, check the value of success, if it is 100 that means that all prisoners have been successful.
If success = 100 Then
Cells(try, 5).Value = “Complete”
Else
‘if it was an overall failure, mark it as such and list the number of prisoners who did find their
‘own number, the value stored in “success”
Cells(try, 5).Value = “Fail”
Cells(try, 6).Value = success
End If
‘reset the success variabel, shuffle the box numbers that the prisoners will check in preparation of the next simulation,
‘shuffle the papers in the boxes, and increase “try” by one as the next simulation is about to begin
success = 0
Call shuffleBoxes
Call shuffle
try = try + 1
Loop
End Sub
Sub shuffle()
Randomize
Dim x As Long
Dim numbers As New Collection
For x = 1 To 100
numbers.Add x
Next x
For y = 1 To 100
rando = WorksheetFunction.RandBetween(1, numbers.Count)
Sheets(“Main”).Cells(y, 2).Value = numbers(rando)
numbers.Remove (rando)
Next y
End Sub
Sub shuffleBoxes()
Dim x As Long
Dim numbers As New Collection
Dim num(0 To 99) As Variant
For x = 1 To 100
numbers.Add x
Next x
y = 1
Do Until y > 100
rando = WorksheetFunction.RandBetween(1, numbers.Count)
num(y – 1) = numbers(rando)
numbers.Remove (rando)
Sheets(“RandomListForPrisoners”).Cells(y, 1).Value = num(y – 1)
y = y + 1
Loop
End Sub